What even is a Tree Data Structure?
A tree is a special type of hierarchical data structure that is connected and does not contain any closed paths. This helps you to store information easily in a hierarchical layout.
Depending on whether the edges of the tree have an uniform direction or not, the tree can be an undirected tree, a directed tree, or an Arborescence. (By the way, if you don't already know. When i say edges i refer to the lines between the dots and when i say nodes i mean the dots)
And there also is the programmers favorite - the Binary tree which is an Arborescence in which a parent node can only have a maximum of two child nodes.
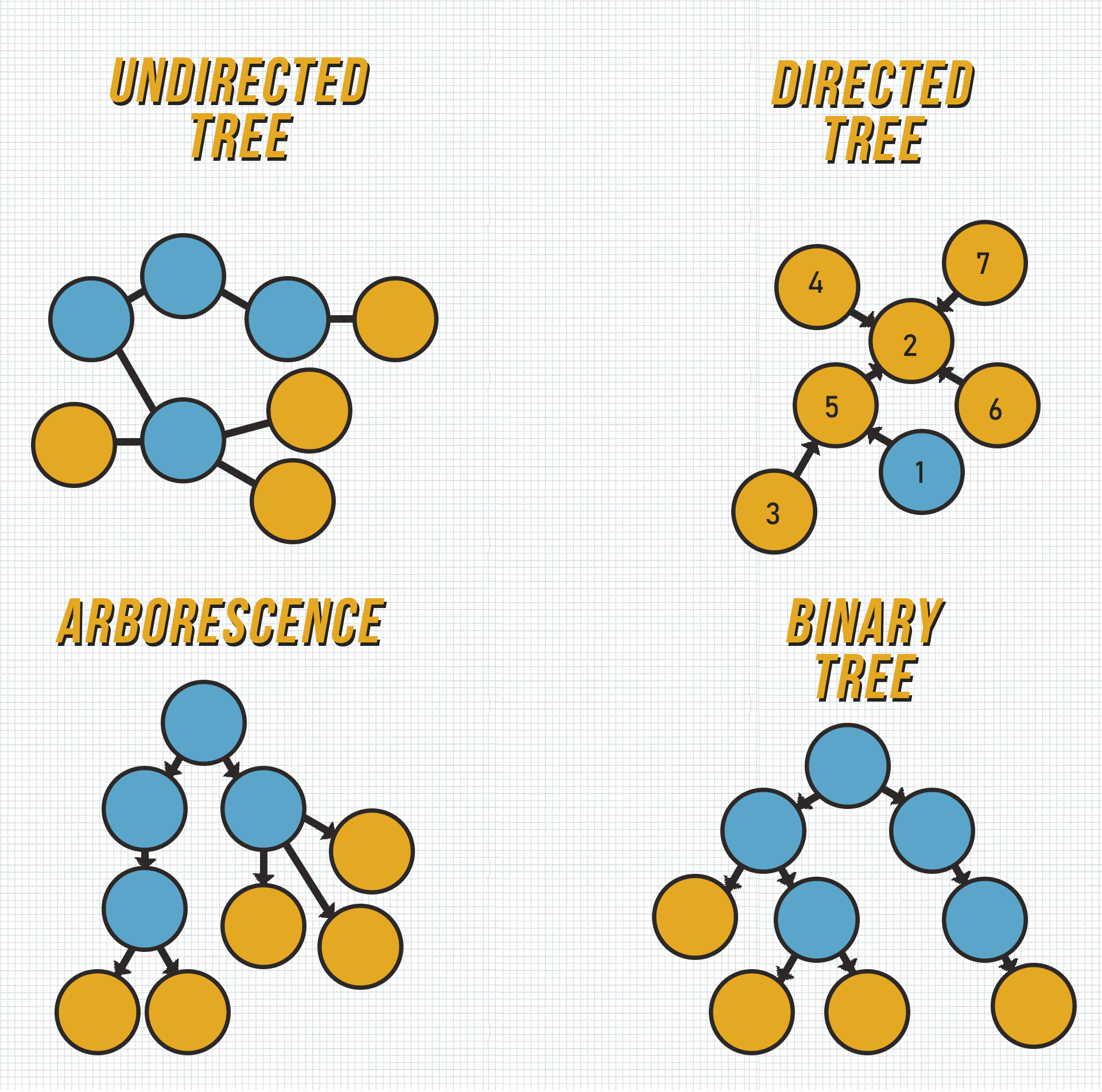
Undirected Tree
In graph theory, an undirected tree is a special tree whose edges have no direction. The undirected tree does not have a parent root, opposed to directed trees.
Directed Tree
A directed tree (also called in-tree or anti-arborescence) in graph theory is a tree that has a parent node, a root, from which all other nodes can be reached, or which can be reached from any other node.
Arborescence
The Arborescence (also called out-tree) is a directed graph with a root, which, in contrast to an undirected tree, refers to the fact that each node can be reached from the root and unlike an Directed Tree, there is only one directed path which can be reached from the root.
Binary Tree
Binary trees are the most widely used types of trees in computer science. Unlike other types of trees, the nodes of a binary tree can only have a maximum of two direct children.
It is typically required that the child nodes have to be clearly divided into left and right children. An illustrative example of such a binary tree is the pedigree, in which, a child only ever has a father and a mother.
17+ Binary Tree Based Coding Problems for Interviews
Now that you know the types of trees - especially Binary Trees, here's a list of common and popular binary-tree-based coding questions from developer / software engineers job interviews:
- How can you implement a binary search tree? (answer)
- How can you implement a Iterative & Recursive preorder traversal in a binary tree? (answer)
- How can you traverse a binary tree without recursion in preorder? (answer)
- How can you find the Minimum Depth of a Binary Tree? (answer)
- How can you implement a postorder traversal algorithm? (answer)
- How can you print all leaves of a binary search tree? (answer)
- How can you print all nodes of a binary tree using inorder traversal without recursion? (answer)
- How can you count the number of leaf's in a binary tree? (answer)
- Write a program to verify whether a binary tree is a full binary tree or not (answer)
- What is a Depth First Search Algorithm for a binary tree? (answer)
- How can you convert a binary tree to a doubly linked list? (answer)
- What is a self balancing binary tree? (answer)
- What is an AVL Tree and How can you implement one? (answer)
- How can you convert a binary tree to a binary search tree? (answer)
- Find the largest BST subtree of a binary tree (answer)
- Check if a binary tree is a subtree of another binary tree (answer)
- Write a program to connect nodes at the same level of a binary tree (answer)
- What is a Trie data structure and what is the difference to a Binary tree ? (answer)
Conclusion
These are some of the most common and important questions about the binary tree data structure from coding interviews that will help you to do well in your coding interview.
But it's not enough to only know about binary trees. You should also check out some other common questions about data structure's of interviews here. The level of the Programming job or the Size of the Company doesn't matter - You will always need to know these common algorithm and data structure questions to be successful at an interview.
Because good knowledge of algorithms and data structures is important to your success in programming interviews, this is where you need to focus most of your attention. The list gives you the right topics to prepare and also helps to evaluate your preparation to find out your strengths and weaknesses.
